Math problems invented on 09/09/2012:
50. Find all triples 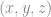 of integers satisfying
of integers satisfying 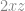 =
= 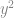 and
and 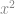 +
+ 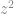 = 2013.
= 2013.
51. In an acute triangle ABC points D, E, F are the feet of the altitudes from A, B and C, respectively. A line through D parallel to EF meets AC at Q and AB at R. Lines BC and EF intersect at P. Prove that the circumcircle of triangle PQR passes through the midpoint of BC. Prove that
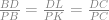 , and ∠PIB = ∠DIP, ∠PJB = ∠DJP.
, and ∠PIB = ∠DIP, ∠PJB = ∠DJP.
52. Let P be a point on the circumscribed circle of ΔABC and H be the orthocenter of ΔABC. Also let D, E and F be the points of intersection of the perpendicular from P to BC, CA and AB, respectively. N = C ∩ BH, Q = C ∩ CH, I = C ∩ PF, J = QC ∩ DF, S = BN ∩ PF, K = BN ∩ AC, T = PE ∩ QC. It is known that the three points D, E and F are collinear. Prove that the line DEF passes through the midpoint of the line segment ST.
53. The sum  +
+  +
+ 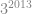 + … +
+ … +  divisible by
divisible by 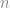 ? Find all possible values for
? Find all possible values for 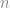 .
.
54.  and
and  are both nine-digit numbers from
are both nine-digit numbers from 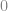 to
to 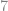 and
and  . Find
. Find  and
and  such that
such that  –
–  =
= 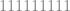 .
.
55. Let ABC be an arbitrary obtuse triangle. Prove that
DG + DH = R + r + DF, where r and R are the inradius and circumradius of triangle ABC, respectively, D the circumcenter of triangle ABC, DF, DG and DH the altitudes to the sides AC, AB and BC, respectively.
56. Points X, Y, Z are marked on the sides AB, BC, CD of the rhombus ABCD, respectively, so that XY || AZ. Let I be the inter-section of AY and XZ. Find the locus of point I.
57. For an acute triangle ABC, let H be the foot of the perpendicular from A to BC. Let M, N be the feet of the perpendicular from H to AB, AC, respectively. Define lA to be the line through A perpendicular to MN and similarly define lB and lC. Show that lA, lB and lC pass through a common point O.
